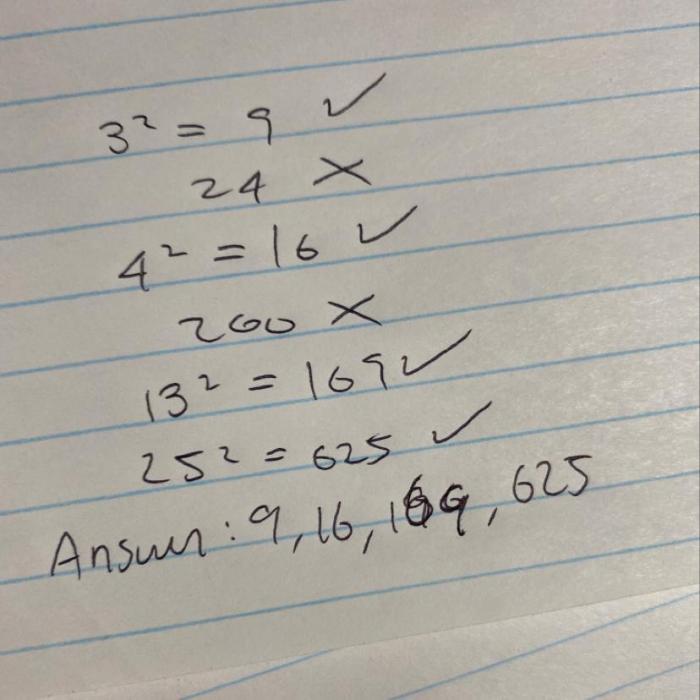Which are perfect squares check all that apply – Perfect squares, numbers that arise from multiplying a whole number by itself, hold a significant place in mathematics and various real-world applications. This exploration delves into the concept of perfect squares, their identification methods, properties, and practical implications, providing a comprehensive understanding of these intriguing numbers.
Understanding perfect squares entails recognizing their defining characteristics, employing effective identification techniques, and exploring their intriguing properties. This discussion unveils the relationship between perfect squares and odd and even numbers, investigates the sum and difference of consecutive perfect squares, and highlights their applications in diverse fields.
Perfect Squares: Which Are Perfect Squares Check All That Apply

Perfect squares are numbers that can be expressed as the product of two equal integers. They are also the squares of whole numbers.
To identify a perfect square, you can use the following methods:
Square Root Method, Which are perfect squares check all that apply
The square root of a perfect square is a whole number. For example, the square root of 16 is 4, and 4^2 = 16.
Prime Factorization Method
A perfect square can be expressed as the product of two equal prime numbers. For example, 16 can be expressed as 2^4, and 2 is a prime number.
Trial and Error Method
You can also use trial and error to identify perfect squares. Start by multiplying a whole number by itself. If the result is a perfect square, then the original number is a perfect square.
Perfect squares have several interesting properties:
Relationship to Odd and Even Numbers
The square of an odd number is always odd. The square of an even number is always even.
Sum and Difference of Consecutive Perfect Squares
The sum of two consecutive perfect squares is always odd. The difference of two consecutive perfect squares is always a multiple of 8.
Applications in Mathematics and Real-Life Situations
Perfect squares have many applications in mathematics and real-life situations. For example, they are used in architecture, engineering, and physics.
Here are some examples of perfect squares in real-life applications:
Architecture and Design
Perfect squares are often used in architecture and design to create symmetrical and aesthetically pleasing structures.
Engineering and Construction
Perfect squares are used in engineering and construction to calculate the strength and stability of structures.
Physics and Acoustics
Perfect squares are used in physics and acoustics to calculate the frequency of sound waves and the resonance of musical instruments.
Table of Perfect Squares
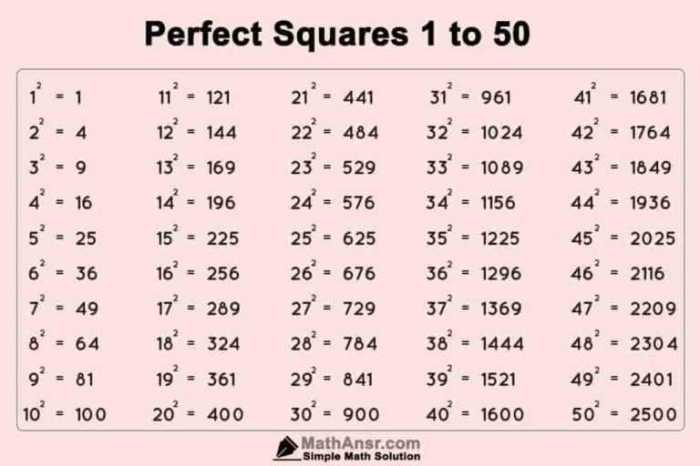
The following table lists perfect squares from 1 to 100:
| Number | Perfect Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 7 |
| 8 | 64 | 8 |
| 9 | 81 | 9 |
| 10 | 100 | 10 |
Perfect Squares and Prime Numbers

Perfect squares and prime numbers have an interesting relationship. Every prime number is either a perfect square or can be expressed as the sum of two perfect squares.
The Goldbach conjecture states that every even number greater than 2 can be expressed as the sum of two prime numbers. This conjecture has not yet been proven, but it is widely believed to be true.
Key Questions Answered
What is the definition of a perfect square?
A perfect square is a number that can be expressed as the product of two equal whole numbers.
How can I identify perfect squares?
Perfect squares can be identified using methods like the square root method, prime factorization method, or trial and error method.
What are some properties of perfect squares?
Perfect squares have various properties, including their relationship with odd and even numbers, the sum and difference of consecutive perfect squares, and their applications in mathematics and real-life situations.