Embark on an educational journey with our comprehensive Area and Circumference Formulas Worksheet. Delve into the fundamental concepts of area and circumference, unlocking their practical applications in real-world scenarios. This meticulously crafted worksheet empowers you to master these essential formulas, equipping you with the knowledge and skills to solve complex problems with confidence.

As we delve deeper into this exploration, we will uncover the formulas for calculating the area of circles, rectangles, and triangles. We will also unravel the intricacies of circumference formulas, exploring the relationship between the radius and diameter of circles.

With a blend of theoretical explanations and practical exercises, this worksheet promises an immersive and enriching learning experience.

Area and Circumference Concepts

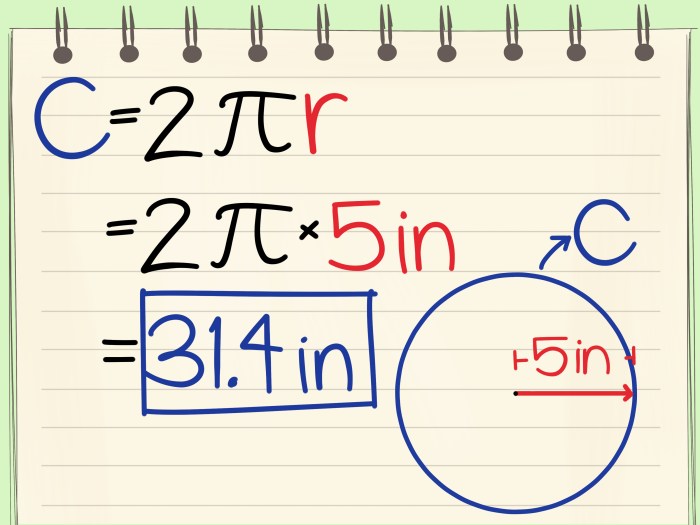
Area and circumference are two important geometric measurements that are used to describe the size and shape of objects. Area is the measure of the surface of a two-dimensional object, while circumference is the measure of the distance around the perimeter of a two-dimensional object.

Area and circumference are used in a variety of real-world applications, such as:

• Calculating the amount of paint needed to cover a wall
• Determining the amount of fabric needed to make a dress
• Calculating the distance around a track
• Measuring the area of a field

Area Formulas

The formula for calculating the area of a circle is:

A = πr ²

where A is the area of the circle and r is the radius of the circle.

The formula for finding the area of a rectangle is:

A = lw

where A is the area of the rectangle, l is the length of the rectangle, and w is the width of the rectangle.

The formula for determining the area of a triangle is:

A = (1/2)bh

where A is the area of the triangle, b is the base of the triangle, and h is the height of the triangle.

Circumference Formulas, Area and circumference formulas worksheet

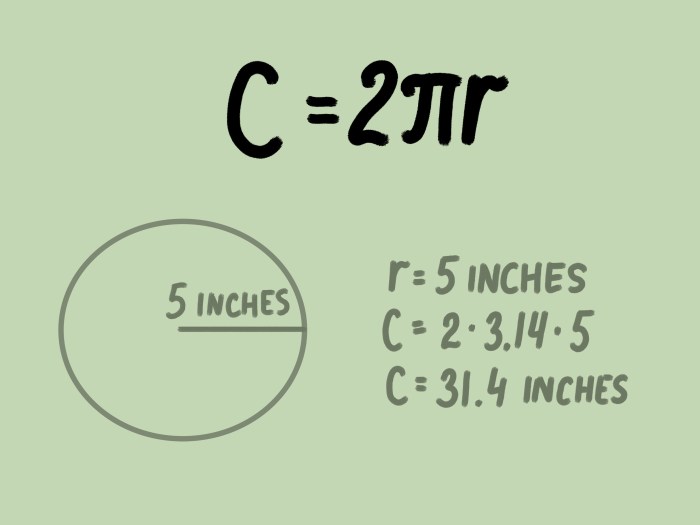
The formula for calculating the circumference of a circle is:

C = 2πr

where C is the circumference of the circle and r is the radius of the circle.

For example, if a circle has a radius of 5 cm, then its circumference would be:

C = 2π(5 cm) = 10π cm

The relationship between the radius and diameter of a circle and how it affects the circumference is that the circumference of a circle is directly proportional to its diameter. This means that if the diameter of a circle is doubled, then its circumference will also be doubled.

Q&A: Area And Circumference Formulas Worksheet

What is the formula for calculating the area of a circle?

A = πr², where A is the area and r is the radius of the circle.

How do I find the circumference of a rectangle?

C = 2(l + w), where C is the circumference, l is the length, and w is the width of the rectangle.

What is the relationship between the radius and diameter of a circle?

The diameter of a circle is twice its radius (d = 2r).